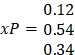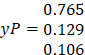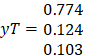CAPÍTULO
I. SISTEMAS IDEALES
Contenido
1. Sustancias
puras
1.1. Propiedades
de las sustancias puras
1.1.1. Propiedades generalizadas
1.1.2. El agua: ecuaciones de González Pozo
1.1.3. Estimación de propiedades de saturación con Excel
1.2. Funciones de estado
1.3. Criterios
de equilibrio líquido vapor
1.3.1. Condiciones
para el ELV
2. Sistemas
multicomponentes ideales
2.1. Sistemas
binarios
2.2. Ley
de Henry
3. ELV
de sistemas multicomponentes
3.1. Ecuación
de Raoult
3.1.1. Correlación
de Antoine
3.2. Gráficas
de ELV para sistemas binarios
4. Puntos
de rocío y de burbuja
4.1. Presión
de burbuja
4.2. Presión
de rocío
4.4. Temperatura
de rocío
4.5. Estimación
en Excel de puntos de rocío y burbuja
5. Destilación
binaria
5.1. Volatilidad
relativa
5.2. Destilación
instantánea ideal
5.2.1. Línea
de operación de Destilación en la gráfica XY
5.2.2.
Estimación del flasheo en
Excel
7.
ANEXOS
ANEXO 2. Codificación Solver de SMathStudio para evaluar
los puntos de rocío y de burbuja
ANEXO 3. Codificación SMathSolver para resolver la
destilación flash en sistemas ideales.
1.
Sustancias puras
1.1.
Propiedades de las sustancias puras
Todas las sustancias poseen propiedades
básicas llamadas variables de estado como son la presión, temperatura
y volumen con respecto a una cantidad de masa (o moles) y
condicionan la situación de la sustancia en un momento determinado.
Así mismo, poseen entropía
que describe el estado de desorden en que se encuentran la sustancia en un
momento, pero también los sistemas pueden generar entropía debido a los
procesos de cambio a que están sometidos.
Para cada estado (condición determinada
por las propiedades básicas) también existen las funciones de estado, que
describen la cantidad de energía de las sustancias y su disponibilidad y
transferencia. Ellas son
|
energía interna [U] |
|
|
entalpía [H] |
|
|
energía libre de Helmholtz o función
trabajo [A] |
|
|
energía libre de Gibbs [G] |
|
1.1.1.
Propiedades generalizadas
Para la fase gaseosa se puede
considerar comportamiento no ideal y evaluar el volumen utilizando
correlaciones experimentales.
a.
Las
correlaciones generalizadas de Pitzer utilizan las propiedades críticas
de las sustancias y proveen ecuaciones válidas, a presiones y temperaturas
moderadas, para calcular el factor de compresibilidad, y por ende el volumen
específico del gas o vapor.
en
donde ω es el factor acéntrico 
b.
La
correlación de Tsonopoulos para el agua también utiliza las propiedades
críticas
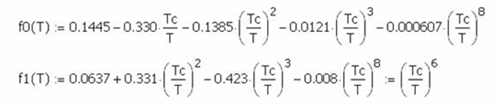
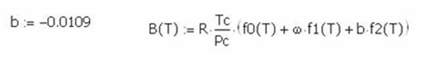
El sistema agua líquida y vapor
saturados se pueden extraer de las Tablas de Vapor, pero también existen
correlaciones experimentales tales como las Ecuaciones de González Pozo
que permiten evaluar el volumen, entalpía y entropía tanto del líquido como del
vapor saturado.
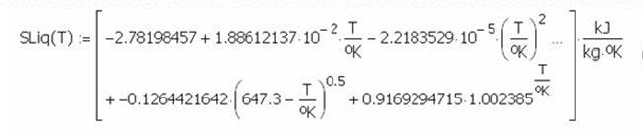
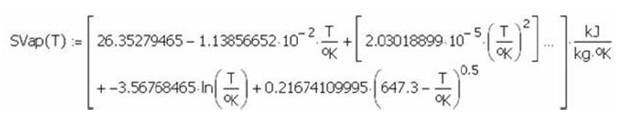
Por ejemplo, asumiendo una
temperatura y aplicando las ecuaciones anteriores
Ejercicio: comparar los resultados
obtenidos con los datos reportados en las tablas de vapor del agua
1.1.3. Estimación de las propiedades
LV con Excel
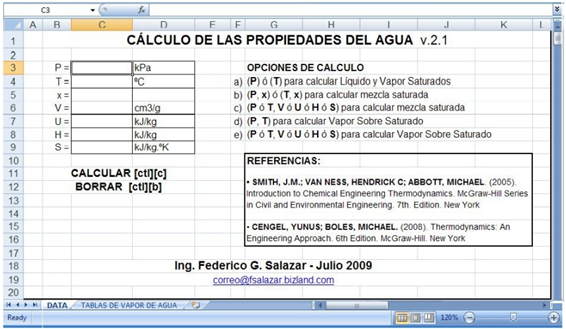
Se pueden obtener las
propiedades del sistema líquido - vapor saturados con las aplicaciones
desarrolladas por el autor, para el agua y para el refrigerante H132A, que se incluyen
a continuación.
Incluyen las aplicaciones desarrolladas
varias opciones de cálculo, dependiendo de la información disponible:
·
Con
solo la presión o la temperatura se obtiene toda la información del LIQ y VAP
saturados
·
Con
la presión o temperatura y la calidad se obtienen las propiedades de la mezcla
saturada
·
Con
la presión o temperatura y otra propiedad diferente de la calidad se obtienen
las propiedades de la mezcla saturada
·
Con
la presión y temperatura se obtienen las propiedades del vapor sobresaturado o
del líquido comprimido/subenfriado
·
Con
la presión o temperatura y otra propiedad diferente de la calidad se obtienen
las propiedades del vapor sobresaturado o del líquido comprimido/subenfriado
TABLAS DE VAPOR DE AGUA EN
EXCEL
TABLAS DE VAPOR DE H134A EN
EXCEL
Las funciones de estado quedan
determinadas por la relación de las propiedades, tal como se puede ver en las
siguientes ecuaciones que las definen
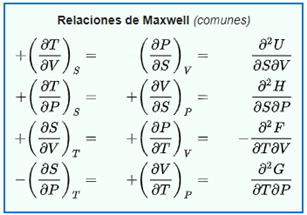
Las relaciones termodinámicas de
Maxwell son un conjunto de ecuaciones termodinámicas que se derivan del teorema de Clairaut o Schwarz (teorema de la
igualdad de las derivadas cruzadas o segundas derivadas) y de las definiciones
de los potenciales
termodinámicos o
funciones de estado asociados a un sistema termodinámico con dimensiones
de energía potencial. Estas relaciones se denominan así (¡los monstruitos de
Maxwell!) por el físico del siglo XIX James Clerk Maxwell.
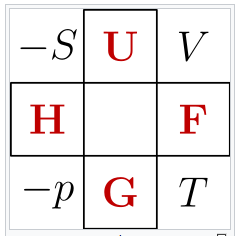
Con el diagrama de Max Born se pueden determinar
las relaciones termodinámicas de Maxwell. Se sugiere consultar a Kim & Selvaraj (2016)
que muestra cómo obtenerlas.
|
Fig. 1. Cuadro termodinámico que
relaciona las variables térmicas y mecánicas del sistema |
|
|
|
|
|
Fuente: Wikipedia (2022) |
|
Utilizando el nemónico se puede
determinar la energía libre de Gibbs, que es la energía que puede
utilizarse para hacer trabajo
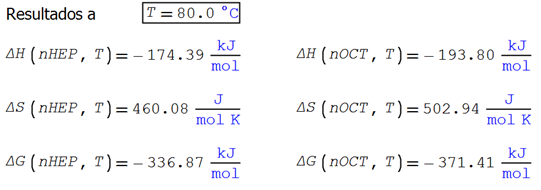
Ilustración. Evaluar las funciones de
estado para el n-heptano y el n-octano, que se encuentran a la temperatura de 50°C
y 1 atmósfera.
Solución. Se dispone de la siguiente
data de tablas
La expresión desarrollada de la capacidad calorífica en función de la
temperatura para cada componente
La entalpía, entropía y energía libre
pueden calcularse para cada componente puro en función de la temperatura
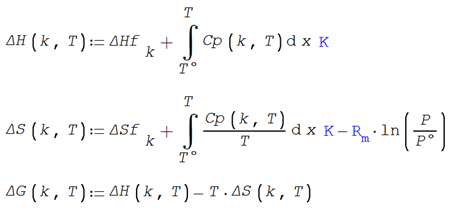
La energía libre de Gibbs para una
mezcla binaria ideal se evalúa con la siguiente expresión función de la
temperatura y la composición de cada componente
Se
han desarrollado correlaciones experimentales que permiten fácilmente obtener
los valores de las propiedades para condiciones dadas.
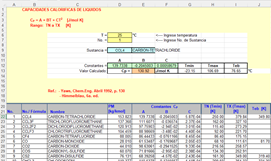
Para una amplia gama de
compuestos orgánicos se incluye en Excel la tabla de constantes de la capacidad
calorífica en fase líquida.
1.3.
Equilibrio de fases LV en sustancias puras
Para un sistema cerrado el análisis de
la energía y entropía del sistema quedan expresadas como
|
Gradiente de energía en un
sistema cerrado |
=
Flujos de calor a través de las paredes del sistema ― Trabajo realizado
por el sistema |
|
Gradiente de entropía en un
sistema cerrado |
=
Flujos de calor respecto a la temperatura del sistema + Entropía generada por
el sistema |
El criterio de equilibrio por la
segunda ley de la termodinámica es 
Para procesos reversibles la generación
de entropía es igual a cero, y la cantidad total de entropía es máxima.
A partir de las relaciones de Maxwell se
establecen los criterios de equilibrio y estabilidad de los sistemas
termodinámicos.
Se presentan varios casos en la
siguiente tabla
Fuente: Sandler (1999)
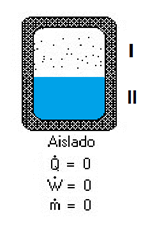
Por ejemplo, para un sistema cerrado y
adiabático en equilibrio, U y V son constantes de tal forma que S = máximo o mínimo en el equilibrio.
Para ese caso, también la temperatura y
presión permanecen constantes si no hay reacción química. Y la energía libre de
Gibbs G = mínima
Este criterio puede aplicarse para
sistemas cerrados y adiabáticos en donde coexistan varias fases en equilibrio.
|
|
ntot
= nI + nII Utot
= UI + UII Vtot
= VI + VII Stot
= SI + SII TI
= TII PI
= PII GI
= GII |
A
partir de la consideración que para el equilibrio la energía libre de Gibbs es
igual para cada fase presente, y por la definición canónica de la energía de
Gibbs se desarrolla la llamada Ecuación de Clapeyron
en donde Psat = presión
de saturación
T = temperatura del sistema
ΔHvap = entalpía de vaporización
ΔVfase = gradiente de volumen por
cambio de fase
Esta ecuación sirve para calcular el
calor de vaporización a partir del cambio en las propiedades del sistema.
1.3.1. Condiciones de
equilibrio LV
Para establecer las condiciones
del ELV en sustancias puras se definen las fracciones en volumen de ambas fases
zL y zG, y suman la unidad
zL + zG = 1
Si se conoce el volumen del sistema V,
podemos decir que:
vT = zL . vL + zG . vG
en donde vT = volumen especifico total del sistema
vL = volumen específico
de la fase líquida
vG = volumen específico de la fase vapor
Ilustración. Un cilindro cerrado de 3 m3
contiene agua a 100°C y 101.325 kPa. Se sabe que la masa total del agua dentro
del cilindro es de 1.8 kg. Se desea determinar las fracciones en volumen de
ambas fases dentro del cilindro.
Solución. De las tablas de
vapor de pueden obtener los volúmenes específicos de saturación para ambas
fases LV a las condiciones del sistema.
Directamente se obtienen las
fracciones volumen de ambas fases
Por
la definición de calidad del vapor hallamos la masa de cada fase
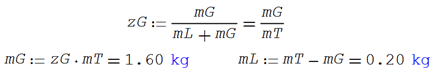
Igualmente,
se pueden evaluar las funciones de estado
Comprobando
las condiciones del equilibrio de fases
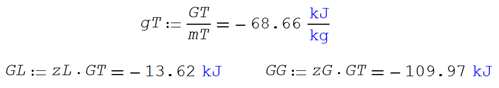
2. Sistemas multicomponentes
En algunas oportunidades se
puede evaluar las condiciones del equilibrio líquido vapor realizando una idealización
del sistema, cuando las cantidades de alguno de los componentes presentes
tiende a cero, es decir, para concentraciones muy diluidas o concentradas.
Realizaremos un breve
análisis para sistemas binarios. En estos casos, independientemente de la no
idealidad de un sistema se le puede considerar ideal para esos niveles límite
de composición de alguna de las sustancias presentes. Y esto se explica
fácilmente en el sentido que a menor presencia de moléculas “extrañas” en el
seno de un líquido, menor será su desviación de la idealidad, ya que el sistema
en su conjunto no llega a verse afectado en mayor grado por la presencia de
esas pocas moléculas del otro componente.
En los sistemas binarios el
ELV se puede expresar en términos de la Constante de Henry o la de Lewis
Randall, dependiendo del grado de concentración y del análisis que se esté
realizando sobre el sistema. Se muestra en la figura esta idealización que en
la práctica conduce a estimar el ELV de forma muy sencilla. Las bebidas
gaseosas son un ejemplo cotidiano de la ley de Henry en donde la cantidad de
gas disuelto en el equilibrio es muy poca.
La Ley de Henry define que
“la cantidad de aire disuelto en un fluido es proporcional a la presión del
sistema”. Tal como comenta Volland (2011), teniendo en cuenta que la
solubilidad de un gas en un líquido es función de la temperatura del sistema,
la presión parcial del gas sobre el líquido (es decir, su concentración en la
fase volátil), la naturaleza del solvente y la naturaleza del gas, la constante
de Henry puede evaluarse en términos de la solubilidad de un gas en un
determinado solvente.
Fig. No. 1. Ley de Henry y Regla de Lewis para el sistema acetona
– cloroformo a 25°C
Adaptado de https://compuestosite.blogspot.com/2021/09/ley-de-henry-ejemplos.html
Dado que el solvente más
común es el agua, se encuentra extensa información en la bibliografía, para los
sistemas de agua y diversos solventes compatibles.
Para predecir el ELV resulta un tipo de expresión
simplificada. Es especialmente válida para sistemas con solutos a dilución muy
pequeña o infinita. Se expresa en términos de la constante de Henry
en donde i = sustancia 1 o 2
xi = fracción de la sustancia en el líquido
yi = fracción de la sustancia en el gas
kHi = constante de Henry de la sustancia
P = presión total del sistema
La ecuación anterior puede
definirse en términos de la concentración del soluto y su presión parcial
ejercida a una temperatura contante
en donde Pgas
= presión del gas
Cliq
= solubilidad del gas en el líquido
Para cada sistema binario,
la constante de Henry es diferente y depende de las propiedades de cada gas y el
disolvente presente en la mezcla. Es además, función de la temperatura, y sus
unidades dimensionales dependen de las unidades utilizadas para la
concentración y presión.
Para una temperatura fija el
valor de kH es el mismo, lo que implica que la relación de concentraciones es
igual a la relación de presiones para dos mezclas diferentes.
La siguiente ecuación puede
utilizarse para relacionar los cambios de presión y concentración de dos
soluciones a la misma temperatura.
en donde Cliq1
= solubilidad de la sustancia 1 a la presión 1
Cliq2
= solubilidad de la sustancia 2 a la presión 2
Pgas1
= presión en el gas de la solución 1
Pgas2
= presión en el gas de la solución 2
Ilustración.
Calcular la cantidad de aire disuelto en agua a 25ºC. La información disponible
es la siguiente
Solución.
La concentración de ambos gases se puede calcular a partir de la
relación
El oxígeno disuelto en agua a la presión atmosférica es
Y el nitrógeno disuelto
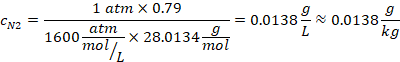
Dado que el aire es la suma de nitrógeno y el oxígeno presentes
Calculando el aire disuelto
en agua a otras presiones y a la misma temperatura 25°C se obtienen los
siguientes valores y la gráfica correspondiente
Fig. No. 2. Oxígeno disuelto en agua fresca
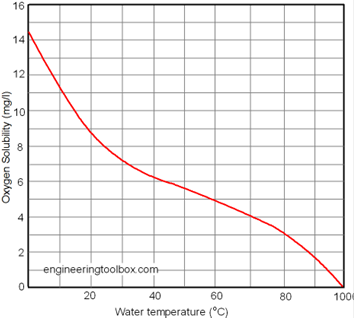
Fuente: The Engineering ToolsBox
Por otra parte, en analogía
para sistemas con la ley de Henry, a concentraciones muy altas, tendiendo a
uno, el ELV queda expresado el equilibrio en términos de la Regla de Lewis
Randall así
en donde i
= sustancia 1 o 2
xi = fracción de la sustancia en el líquido
yi = fracción de la sustancia en el gas
kLRi = constante de Lewis Randall
P = presión total del sistema
Ejercicio: evaluar para el sistema
acetona – cloroformo de la figura 1, el equilibrio para 0.20 y 0.80 de
cloroformo, tomando de esa gráfica los valores de la constante de Henry y la de
Lewis Randall.
En la bibliografía se reportan otras relaciones de concentración, por
ejemplo el oxígeno disuelto en agua a diferentes temperaturas. Se muestra en la Tabla No. 1 diversos valores de la solubilidad del aire
en agua a diferentes temperaturas y presiones.
Tabla
No. 1. Solubilidad del aire en agua
[vol Aire / vol. Agua]
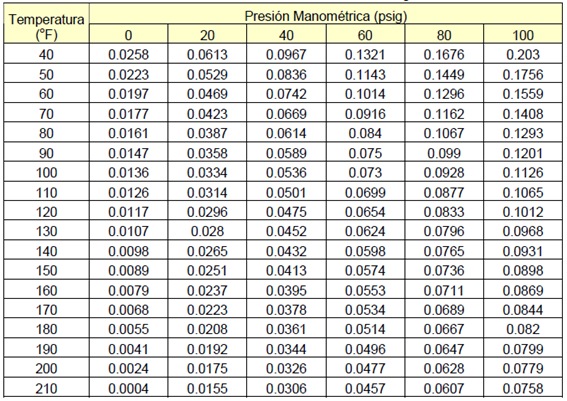
Tomado de The Engineering ToolsBox (2004)
Estas gráficas (fig.
3) son nomogramas que presentan las constantes experimentales del equilibrio líquido
vapor de los hidrocarburos más simples. Fueron desarrolladas en la industria
del petróleo, sobre datos reales, para realizar evaluaciones rápidas del
equilibrio.
Expresan en
principio la relación de fases para el equilibrio experimental de hidrocarburos
simples
en donde i
= sustancia en el sistema
xi = fracción de la sustancia en el líquido
yi = fracción de la sustancia en el gas
Ki = constante de DePriester
P = presión total del sistema
Su modo de
empleo consiste en asumir una propiedad de mezcla. Por ejemplo, la temperatura,
para una presión y composición de una fase dadas. Trazando líneas rectas entre
la propiedad conocida y la asumida se leen los valores correspondientes de Ki
para cada componente participante en la mezcla.
Se hace una
comprobación de la correlación utilizando la ecuación mostrada antes y en caso
de no tener convergencia se asume un nuevo valor de la propiedad buscada, hasta
lograr la convergencia buscada.
Ilustración. Para el sistema binario
isobutano (1) / n-heptano (2) a 500 kPa se desea evaluar su temperatura de
burbuja cuando la composición del isobutano en el líquido es del 15% molar.
Solución. El procedimiento sugerido
es:
1. se ubica la presión de operación en la gráfica de DePriester
2. se asume una temperatura de burbuja. En este caso 180ºC (trazo rojo en
la figura no. 3)
3.
se traza una línea recta
que unen ambos valores
4.
se leen las constantes de
equilibrio correspondientes para cada componente: k1 = 7.6 y k2 = 1.16
5. se aplica la ecuación de equilibrio para evaluar las composiciones en la
fase gaseosa: y1 = 1.14 e y2 = 0.986
6. la suma de los valores hallados deberá ser la unidad. En caso negativo
se asume un nuevo valor de temperatura y se regresa al paso 2 hasta hallar
convergencia.
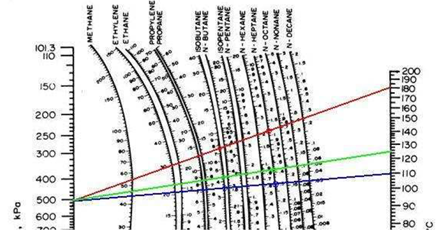
Fig. 3.
Grafica de DePriester de Constantes de ELV
Fuente: Smith, van Ness & Abbott (2007)
2a. Asumimos 110ºC.
3a. trazamos la línea recta (trazo azul en la
figura no. 3a)
4a. se leen ahora los valores k1 = 3.15 y k2 = 0.245
5a. al aplicar la ec (5) y1 = 0.4725 e y2 = 0.2083
6a. dado que la suma ahora es menor que la
unidad, se vuelve al inciso 2
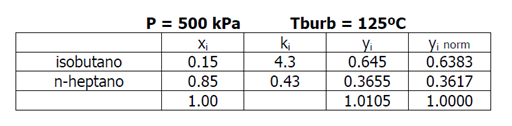
2b. Asumimos 125ºC.
3b. trazamos la línea recta (trazo verde en
la figura no. 3a)
4b. se leen ahora los valores k1 = 4.3 y k2 = 0.43
5b. al aplicar la ec (5) y1 = 0.645 e y2 = 0.3655
6b. la suma da aproximadamente 1.01. Adoptamos esta solución con un
margen de error del 1%
7. finalmente podemos normalizar dichos valores
para que la suma nos de la unidad: 0.6383 y 0.3617
Fig. No. 3a.
Detalle de la Gráfica de DePriester
El resultado por
iteraciones se muestra en la siguiente tabla
3.
Sistemas Multicomponentes Ideales
Es una ley termodinámica que establece que en una mezcla ideal de líquidos, la presión parcial en el vapor de cada componente es igual a la presión de vapor del
componente puro multiplicado por su fracción molar en la mezcla líquida.
en donde i = sustancia i en la mezcla
multicomponente
xi = fracción molar de la sustancia en el líquido
yi = fracción molar de la sustancia en el vapor
Pvapi = presión de vapor de la sustancia i, f(T)
P = presión total del sistema
La importancia de esta ley es que describe y
relaciona, para sistemas multicomponentes ideales, las concentraciones en el
líquido y las del vapor, la presión total del sistema y su temperatura a través
de la presión de vapor.
Combinando la ley de Raoult con la ley de Dalton de las presiones
parciales se obtiene
En consecuencia, la presión total del sistema es 
Para sistemas binarios la relación se
simplifica
Esta ecuación corresponde a
una línea recta, y en una gráfica de composición molar en el líquido contra la presión
total del sistema tiene la siguiente forma
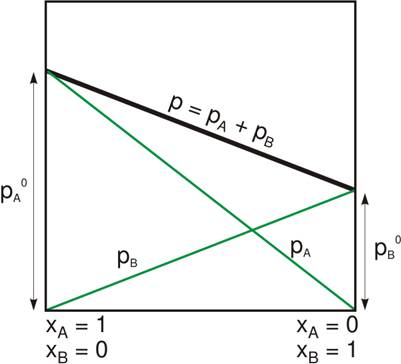
Fuente: Wikipedia
P es la presión total para
diferentes composiciones de la mezcla y pa y pb las
presiones parciales de cada componente.
De la ecuación anterior se
obtiene una expresión para la fracción molar
De la ecuación de Clapeyron mencionada en el inciso
1.2 se puede derivar la respectiva Ecuación de Clausius-Clapeyron
en donde Pvap
= presión de vapor de la sustancia, f(T)
T = temperatura del sistema
ΔHvap = calor de vaporización de
la sustancia
R = constante universal de los gases
Haciendo una integración
indefinida de la ecuación anterior se obtiene
A partir de la integración
anterior se obtuvo la Ecuación de Antoine
en donde Pvap
= presión de vapor de la sustancia, f(T)
T = temperatura del sistema
A, B, C = constantes a partir de
las propiedades de la sustancia
Esta ecuación
es usada para correlacionar la presión de vapor con bastante exactitud entre
rangos de 1 a 200 kPa en función de la temperatura.
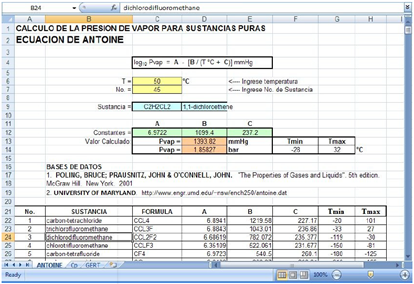
CALCULO DE LA PRESION DE
VAPOR
CONSTANTES DE ANTOINE
3.2.
Gráfica ELV para sistemas binarios
Utilizando la ecuación de Raoult y aplicando la ecuación de Antoine se
pueden construir fácilmente las gráficas de equilibrio de composición contra la
temperatura del sistema para sistemas ideales binarios.
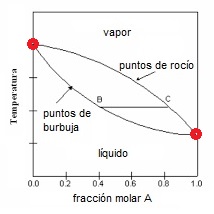
La gráfica parte de la temperatura
de vapor de B puro ( xA = 0 ) y termina con la temperatura de vapor
de A puro ( xA = 1 ).
Se generan las curvas de
equilibrio de la fase líquida con los puntos de burbuja y la fase vapor con los
puntos de rocío.
La otra gráfica equivalente corresponde a la gráfica de equilibrio de
composición contra la presión del sistema para sistemas ideales binarios.
En este caso la gráfica
parte de la presión de vapor de B puro ( xA = 0 ) y termina con la
presión de vapor de A puro ( xA = 1 ).
Se generan igualmente dos
curvas de equilibrio de la fase líquida y la fase vapor en función de la
presión.
Ilustración. Para el sistema ideal
n-heptano (A) y n-octano (B) a las siguientes condiciones
Psist = 650 mmHg T = 378°K
Para encontrar los valores límite de temperatura (sustancias puras) se
utiliza la ecuación de Antoine asumiendo que la presión del sistema corresponde
a la presión de vapor de la sustancia pura. Despejando la temperatura tenemos
La temperatura de saturación del n-heptano (A) calculada según Poling et
al [mmHg, °C, log]
La temperatura de saturación del n-octano (B)
De la ecuación de Raoult, despejando la composición para el n-heptano
(A) en función de la temperatura
A manera de comprobación, por la definición de presión parcial y la
ecuación de Raoult se pueden evaluar las presiones parciales de ambos
componentes y la presión total, y que efectivamente esta presión calculada
coincide con la presión definida del sistema
Finalmente, se obtiene la
composición de n-heptano en el vapor
Aplicando las relaciones anteriores se obtienen los valores de las
fracciones molares del n-heptano para ambas fases (xA, yA)
en función de la temperatura, que va en el rango de temperaturas de saturación
de ambas sustancias. La presión del sistema permanece constante.
|
T [°C] |
120.12 |
117.67 |
115.22 |
112.77 |
110.32 |
107.87 |
|
xA |
0 |
0.6 |
0.13 |
0.21 |
0.28 |
0.37 |
|
yA |
0 |
0.13 |
0.25 |
0.36 |
0.46 |
0.56 |
|
T [°C] |
105.42 |
102.97 |
100.52 |
98.07 |
95.62 |
93.17 |
|
xA |
0.45 |
0.55 |
0.65 |
0.76 |
0.87 |
1.00 |
|
yA |
0.65 |
0.73 |
0.81 |
0.88 |
0.94 |
0.70 |
Con estos datos de construye la tabla T-xA-yA de
equilibrio ELV para el sistema ideal n-heptano y n-octano.
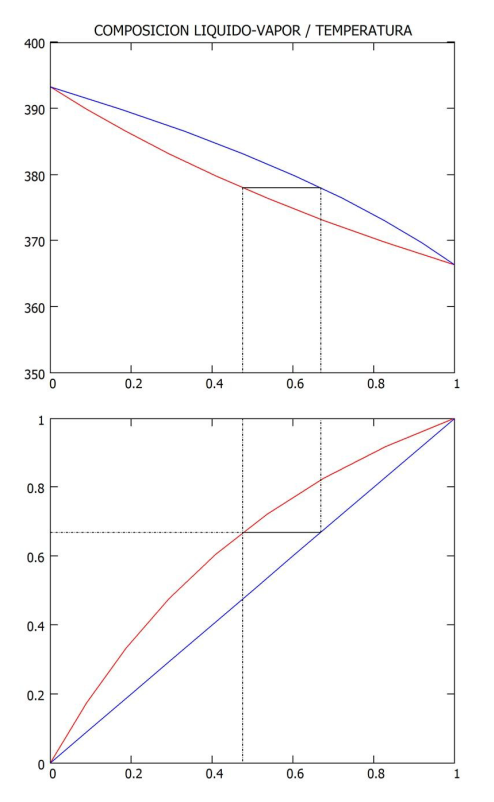
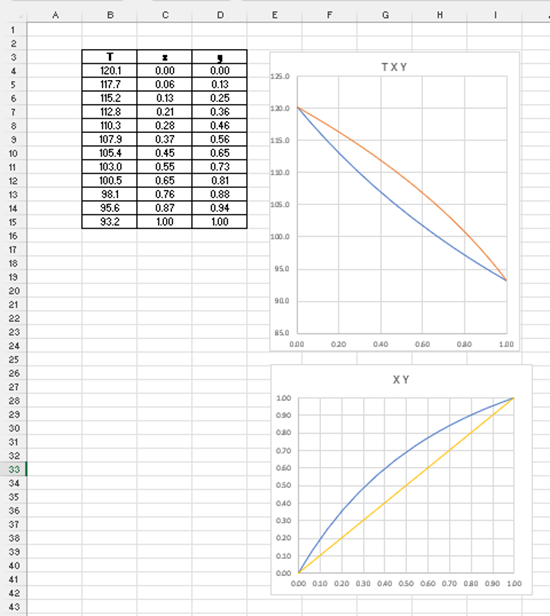
A partir de la gráfica de temperatura-composición se construye la
gráfica del equilibrio xA-yA tal como se muestra a continuación.
En el anexo 1 se incluye la codificación
en SMath Solver en interfase con Excel para obtener graficas de equilibrio
T-x-y a una presión del sistema dada.
4. Puntos de
burbuja y puntos de rocío
Estos puntos corresponden a aquellos estados del sistema para los cuales
existen situaciones de saturación inminente.
Es decir, que la Presión de Rocío representa el momento en el
cual se produce la primera condensación del vapor por descenso de la presión
manteniendo la temperatura constante. Así mismo, la Presión de Burbuja
que corresponde a la descompresión mínima para que hierva un líquido.
Existe consecuentemente, la Temperatura de Rocío será aquella
temperatura mínima a la cual condensa un vapor; y la Temperatura de Burbuja
es la temperatura máxima a partir de la cual inicia la ebullición del líquido.
Los cuatro puntos se muestran sobre las líneas de ELV en las siguientes
gráficas (construidas con MathCAD 2001 Pro).
Para evaluar los puntos de rocío y de burbuja en sistemas ideales se
aplica la Ley de Raoult en equilibrio líquido vapor.
4.1.
Presión de
burbuja
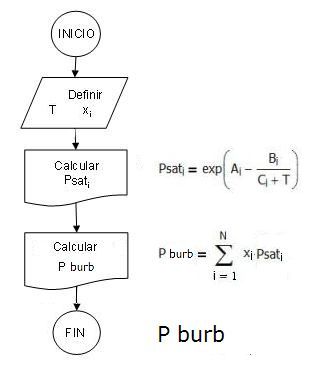
Cuando se conoce la temperatura del sistema, utilizando la Ecuación de
Antoine, se evalúan las presiones de vapor de los componentes del sistema.
Asumiendo o conociendo las composiciones en la fase líquida de calcula
directamente la presión de burbuja aplicando la ecuación que relaciona la
composición en x con las presiones de vapor.
Aplicando de nuevo la ecuación de Raoult para cada componente se
establecen las composiciones de la fase gaseosa.
4.2.
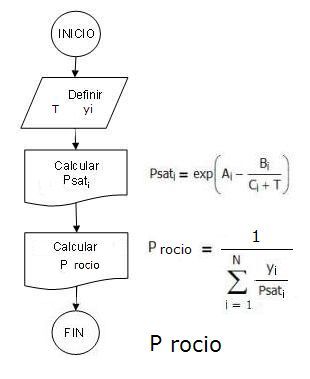Presión de
rocío
Para evaluar la presión de rocío se considera la composición del vapor yi
y con la temperatura se evalúan las presiones de vapor de cada componente.
Utilizando la Ley de Raoult
y el criterio que la sumatoria de xi es igual a uno
Aplicando la ecuación de Raoult a cada componente se establecen las
composiciones de la fase líquida.
Para evaluar la temperatura de burbuja no se puede utilizar directamente
la Ecuación de Antoine para evaluar las presiones de vapor, por lo que es
necesario realizar un proceso iterativo hasta encontrar una convergencia.
En este caso se calculan las temperaturas de saturación de cada componente
arreglando la ecuación de Antoine en función de la presión conocida del
sistema.
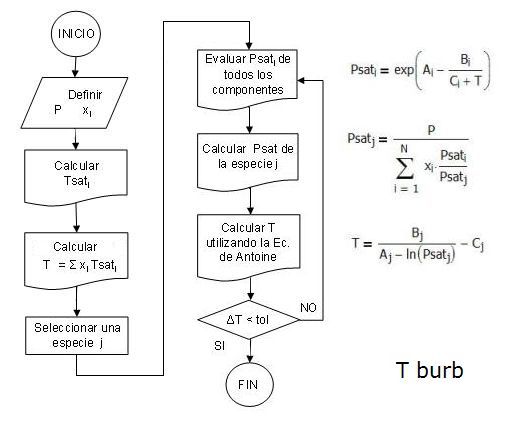
Y se puede hallar un valor semilla de la temperatura del sistema, en
función de las composiciones de la mezcla líquida, que corresponde a la
temperatura de burbuja
Con este cálculo se evalúan las presiones de saturación de los
componentes y tomando como referencia una de las especies presentes se
recalcula la presión de saturación y seguidamente la temperatura del sistema, iterando
hasta hallar la convergencia.
Para evaluar la temperatura de rocío es necesario realizar un proceso
iterativo similar al caso de la temperatura de burbuja
Se calculan las temperaturas de saturación de cada componente en función
de la presión del sistema.
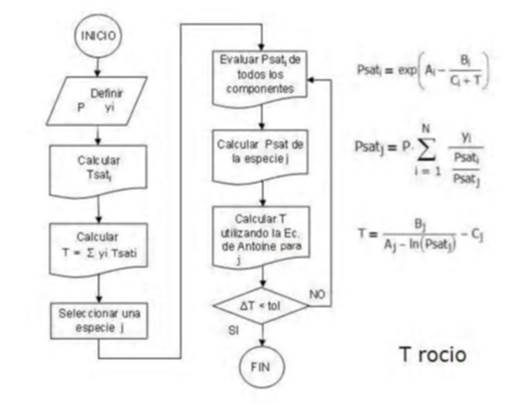
Se halla un valor semilla de la temperatura del sistema en función de
las composiciones del vapor, que corresponde a la temperatura de rocío
Con este valor se evalúan las presiones de saturación de los componentes
y de nuevo con un componente de referencia se recalcula la presión de
saturación y seguidamente la temperatura del sistema, iterando hasta hallar la
convergencia.
Ilustración. Para el sistema ternario ideal acetonitrilo (1) / etilbenceno (2) / clorobenceno (3) en composición de mezcla 0.40, 0.35 y 0.25 respectivamente, estando el sistema a una presión de 70.0 kPa y temperatura de 100.0°C.
Los cuatro puntos de
equilibrio se pueden calcular para las condiciones dadas obteniéndose los
siguientes resultados
|
Procio = 53.2 kPa |
Psist = 70.0 kPa |
Pburb = 93.1 kPa |
|
|
|
|
|
|
|
|
|
Trocio = 108.66 °C |
Tsist = 100°C |
Tburb = 90.54 °C |
Es de notar que ambas temperatura y presión del sistema quedan dentro
del rango de los valores de rocío y de burbuja, y cuando esa condición se da
puede realizarse la operación unitaria de destilación flash, que se discute en
una sección posterior.
En el anexo 2 se incluye la codificación
en SMath Solver para evaluar los cuatros puntos de equilibrio del sistema dado
a presión y temperatura conocidas.
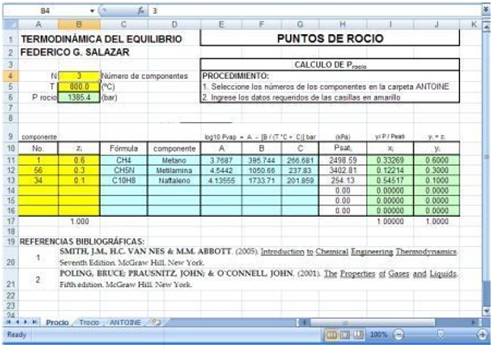
4.5. Estimación en
Excel de puntos de rocío y burbuja
Fueron desarrolladas en Excel dos rutinas para evaluar los puntos de
rocío y de burbuja.
En cada rutina se dejó la opción de adicionar hasta seis componentes de
la mezcla que deberán ser seleccionados dentro del listado de compuestos
disponibles con sus propiedades.
Para evaluar las propiedades en el caso de los puntos de burbuja, que
requieren de iteraciones para obtener una respuesta, se utiliza la función Solver
de Excel de la hoja de cálculo.
PUNTOS DE BURBUJA EN EXCEL
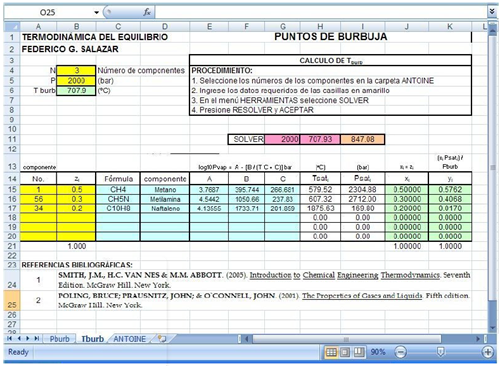
PUNTOS DE ROCIO EN EXCEL
5.
Destilación binaria
La volatilidad relativa es
una medida que compara las presiones de vapor de los componentes en una mezcla
líquida con respecto al componente más volátil.
Esta propiedad se usa
ampliamente en el diseño de los procesos de destilación industrial, puesto que
la fracción de cada componente vaporizándose depende exclusivamente de esta
propiedad, ya que se volatilizarán primero y en mayor cantidad aquel integrante
más volátil de la mezcla.
en donde ref = componente más
volátil
αi,ref
= volatilidad relativa de i con respecto a ref
Para un sistema binario se
tiene 
5.2. Destilación
instantánea ideal
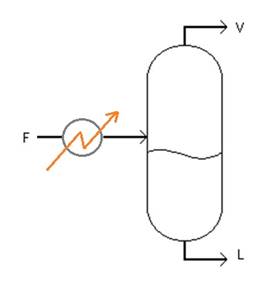También llamada vaporización flash o flasheo, es un proceso de
separación entre fases de los componentes de un flujo (F) sometido a una súbita
descompresión en una cámara adiabática a temperatura y presión de operación
constantes y controladas.
Por efecto del equilibrio
de fases logrado en la descompresión, las composiciones en ambas fases son
diferentes por las diferentes volatilidades relativas de cada una de las
sustancias integrantes de la mezcla.
La temperatura del proceso
es regulada por medio de un intercambiador de calor a la entrada del equipo que
regula las condiciones del flujo ingresando. La presión también puede regularse
siendo la variable que controla la cantidad de vapor formándose.
Se puede resolver
numéricamente por medio de métodos de convergencia, teniendo presente que la
suma de las fracciones molares en cada fase es la unidad, es decir
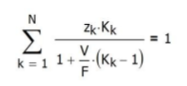
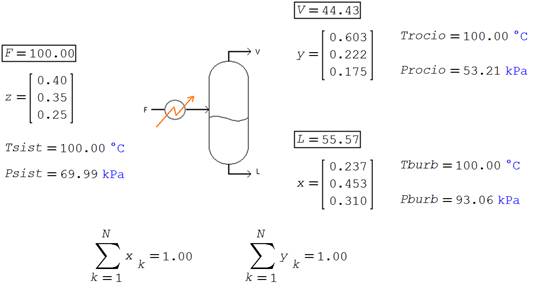
Ilustración. Para el sistema ternario ideal acetonitrilo (1) / etilbenceno (2) / clorobenceno (3) en composición de mezcla 0.40, 0.35 y 0.25 respectivamente, estando el sistema a una presión de 70.0 kPa y temperatura de 100.0°C, determinar si es posible realizar una destilación flash para una alimentación de 100 moles/hr.
Para resolver el problema lo primero que se tiene
que comprobar es si la presión y la temperatura caen dentro del rango de los
puntos de rocío y de burbuja.
En este caso, tal como se indicó en la ilustración
anterior de la sección 4.0 las condiciones del sistema cumplen con el requisito
anterior, y la solución es la siguiente
En el anexo 3 se incluye la codificación
en SMath Solver para resolver la destilación instantánea o flash a las condiciones
del sistema dado de presión y temperatura conocidas.
5.2.1.
Línea de operación de Destilación instantánea
ideal en la gráfica XY
A partir de las ecuaciones 1.39 y 1.40 desarrolladas anteriormente se
obtiene la ecuación característica que describe la Línea de Operación de la
Destilación Instantánea
En donde la pendiente de la línea de operación es –(L/V) en la gráfica
de equilibrio XY
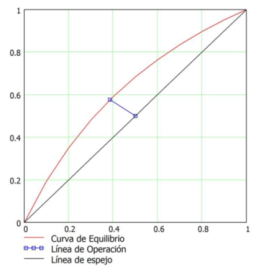
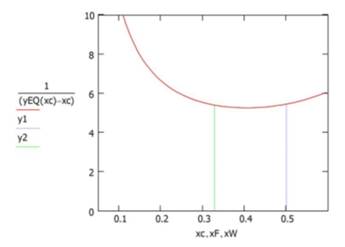
Estableciendo la escala
para la gráfica correspondiente XY, podemos observar la relación existente
entre las líneas de operación y de equilibrio para este proceso de separación
por destilación
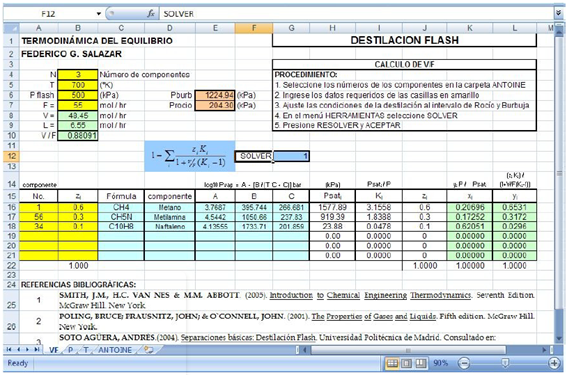
5.2.2. Estimación en
Excel del flasheo
Se desarrolló en Excel una rutina para evaluar la destilación flash
ideal, que permite la opción de adicionar hasta seis componentes de la mezcla
que deberán ser seleccionados dentro del listado de compuestos disponibles con
sus propiedades.
Al igual que la rutina para los puntos de rocío, para evaluar las condiciones
de destilación en los flujos de salida, ya que requieren de iteraciones para
obtener una respuesta, se utiliza la función Solver de la hoja de
cálculo.
DESTILACIÓN FLASH IDEAL EN
EXCEL
5.3.
Destilación diferencial ideal
La destilación diferencial es aquella que se efectúa por tandas, en
donde se carga una mezcla líquida a un recipiente cerrado que posee un sistema
de calentamiento y otro de recuperación y condensación de los vapores
resultantes.
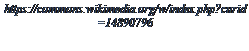El alambique representa tradicionalmente este sistema de destilación en
donde la mezcla se hierve lentamente y los vapores obtenidos son condensados.
|
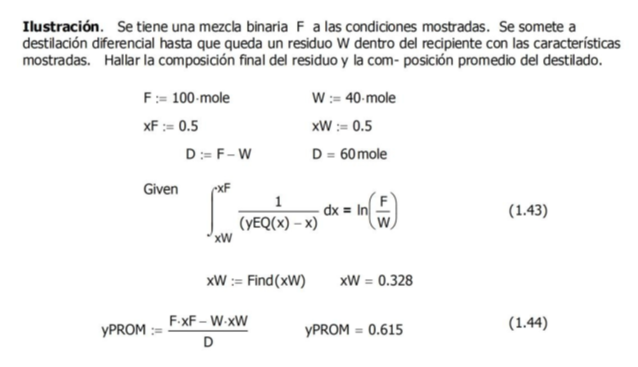
El área bajo la curva entre xInicial = 0.5 xFinal = 0.328 corresponde al logaritmo de
la relación de carga inicial con el residuo final ln(F/W) = 0.92 |
|
|
|
|
·
Engineering ToolBox (2004). Solubility of Air in Water. [online]
Available at:
https://www.engineeringtoolbox.com/air-solubility-water-d_639.html [Accessed 04
junio. 2022].
·
Kim, Younghun
& Selvaraj, Rengaraj (December, 2016). An Improved
Mnemonic Device for Thermodynamic Relations https://www.researchgate.net/publication/316704272_An_Improved_Mnemonic_Device_for_Thermodynamic_Relations/figures?lo=1
·
O’Connell, J.P. &
Haile, J. M. (2005). Thermodynamics:
fundamentals for applications. Cambridge University Press. New York.
·
Poling, Bruce E.;
Prausnitz, John M. & O’Connell, John P. (2000). The Properties of Gases and Liquids. 5th edition.
McGraw Hill. New York.
·
Salazar, Federico G. (2009). Cálculo de las propiedades del agua. https://fgsalazar.net/XLSM/VAPOR_SC_v.3.0.xlsm
·
Salazar, Federico G. (2009a). Cálculo de las propiedades del H134A. https://fgsalazar.net/XLSM/VAPOR_SC%20v.2.1.xlsm
·
Salazar, Federico G. (2009b). Cálculo de las capacidades caloríificas. https://fgsalazar.net/XLSM/CAPACIDAD
CALORIFICA.xlsm
·
Salazar, Federico G. (2011). Cálculo de la presión de vapor y contantes de Antoine. https://fgsalazar.net/XLSM/EQ_ANTOINE.xlsm
·
Salazar, Federico G. (2011b). Flash multicomponente ideal en Excel. https://fgsalazar.net/XLSM/FLASH-IDEAL.xlsm
·
Salazar, Federico G. (2014). Puntos de burbuja en Excel. https://fgsalazar.net/XLSM/BURBUJA.xlsm
·
Salazar, Federico G. (2014a). Puntos de burbuja en Excel. https://fgsalazar.net/XLSM/ROCIO.xlsm
·
Sandller,
Stanley I. (1999).
Chemical and Engineering Thermodynamics. 3rd. edition. John Wiley
& Sons. New York.
·
Smith, J.M; Van Ness, H.C.;
Abbott, M.M. & Swihart, M. T. (2022). “Introduction to Chemical Engineering
Thermodynamics”. 7th edition. McGraw Hill. Boston
·
The Engineering ToolsBox (2012). Air Solubility in Water. Consultado en Internet el día 4 de febrero de 2012 en: http://www.engineeringtoolbox.com/air-solubilitywater-d_639.html
·
Volland,
Volt (2011). Solubility of gases
in liquids. Online Introductory Chemistry. Consultado en
Internet el día 6 de febrero de 2012 en: http://www.800mainstreet.com/9/0009-006-henry.html
·
WIKIPEDIA (2022). Relaciones de Maxwell. https://es.wikipedia.org/wiki/Relaciones_de_Maxwell
·
SMATH
STUDIO. Mathematical program with
WYSIWYG. https://en.smath.com/view/SMathStudio/summary
ANEXOS
ANEXO
1. Codificación SMathSolver en
interfase con Excel para obtener gráficas de temperatura composición de una mezcla
binaria ideal
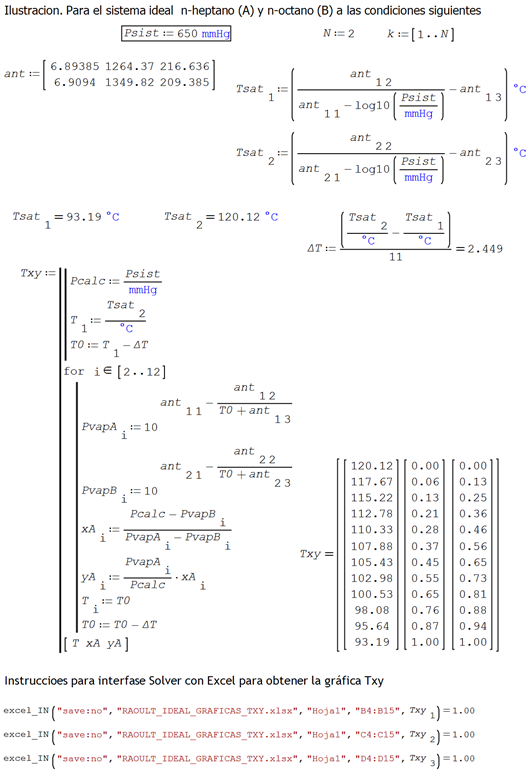
Nombre
del archivo Excel es “RAOULT_IDEAL_GRAFICAS_TXY.xlsx”
que debe estar en el mismo directorio del archivo del solver
ANEXO
2. Codificación SMathSolver para evaluar
los cuatro puntos de equilibrio en sistemas ideales.
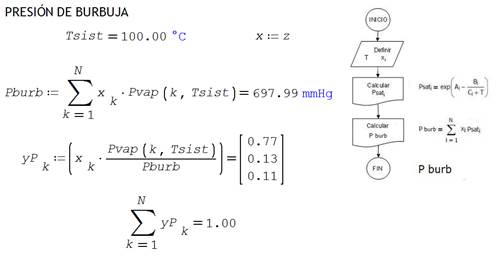
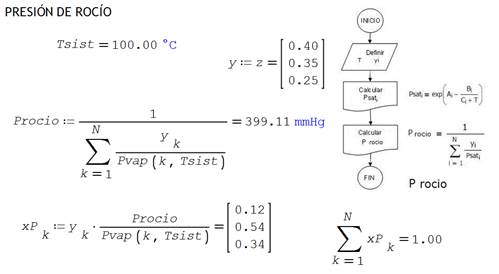
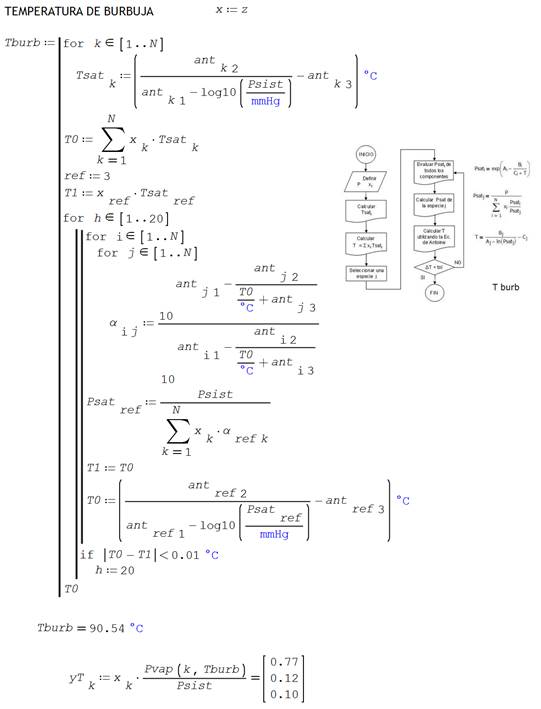
Cuadro
comparativo de resultados
ANEXO
3. Codificación
SMathSolver para resolver la destilación flash en sistemas ideales.
Cuadro
de resultados
